焦茶/夏コミ本に収録です 小宇宙
552 字
3 分钟
二维数组的查找
以前的博客一直处于荒废状态,最近重建,慢慢把以前的笔记还有做过或面试遇到过的算法题重新整理一下。这是刚毕业那会去面试遇到的其中一道笔试题,曾经在牛客网刷过,没有思路会有点难,只能暴力搜索或者对每行进行二分查找,效率比较低,但找到规律后就很简单,在 LeetCode 上是中等难度题 240. 搜索二维矩阵 II
PS:当时边界条件写错,被面试官鞭尸,说这题就差一点,你就被录取了(手写算法太恶心了QAQ),如果当时被录取,我现在就是底边Golang工程师了,不禁让人感叹
题目
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例
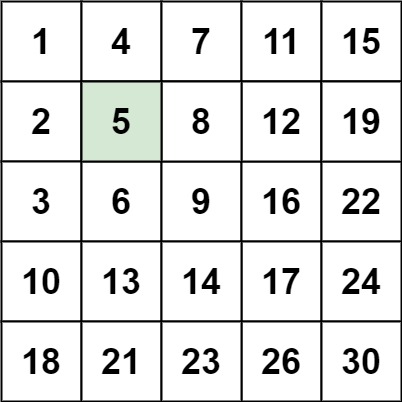
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5输出:true思路
根据题目二维数组的特性,可以发现存在一组对角线,选取任意元素,元素左边都小于当前元素,元素下边都大于当前元素
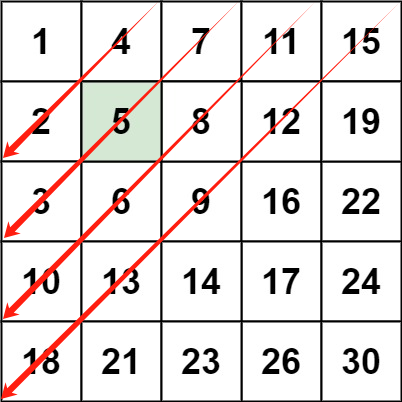
例如:
- 选15,左边11小于15,下边19大于15
- 选8,左边5小于8,下边9大于8
根据这一特性,我们从右上角开始搜索,如果 target 小于当前元素,往左走,反之往下走即可,极限的情况是最左边和最下边都找不到
public boolean searchMatrix(int[][] matrix, int target) { // 判断是否空数组 if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return false; // 指针指向右上角 int i = 0; int j = matrix[0].length - 1; // 边界条件:最左边和最下边都找不到 while (i <= matrix.length - 1 && j >= 0) { // 如果是目标元素,返回 true if (matrix[i][j] == target) { return true; // 如果当前元素大于目标元素,往左走 } else if (matrix[i][j] > target) { j--; // 如果当前元素小于目标元素,往下走 } else { i++; } } // 都没有返回 false return false;}
